Gradien Garis Lurus: Derajat Kemiringan Garis - Hallo sahabat Rumus Matematika, Pada sharing pelajaran kali ini yang berjudul Gradien Garis Lurus: Derajat Kemiringan Garis, saya telah menyediakan contoh soal hingga pembahasan lengkap dari awal pembahasan sampai akhir materi. mudah-mudahan isi postingan tentang pelajaran yang saya tulis ini dapat anda pahami. okelah, ini dia pembahasan nya.

Materi : Gradien Garis Lurus: Derajat Kemiringan Garis
Judul materi : Gradien Garis Lurus: Derajat Kemiringan Garis

Gradien Garis Lurus: Derajat Kemiringan Garis

Perhatikan gambar keempat mobil berikut yang berjalan di jalan: 

Mobil-mobil tersebut sedang melewati jalan yang berbeda-beda. Mobil biru ada di jalan turunan yang cukup curam. Mobil oranye berada pada jalan yang rata dan landai. Mobil merah dan mobil hijau berada pada jalan menanjak tetapi jalan yang dilewati mobil merah jauh lebih landai. Jalan yang dilewati mobil hijau jauh lebih curam. Dalam geometri, untuk menyatakan tingkat kemiringan jalan apakah itu menurun, landai, naik , atau menanjak dinamakan gradien. Jika jalan yang dilewati mobil diatas bisa diandaikan sebagai suatu garis lurus maka gradien secara formal didefinisikan sebagai suatu nilai yang menyatakan derajat kamiringan suatu garis lurus.

Peratikan mobil diatas! Pada saat menanjak mobil sebenarnya bergerak secara horisontal dan juga vertikal yang ditunjukkan pada garis putus-putus merah dan biru. Dengan kata lain, jika mobil bergerak dari A0 menuju A1 itu sama dengan bergerak dari A0 sepanjang garis merah kemudian dilanjutkan dengan melewati garis biru. Menghitung tingkat kemiringan suatu garis lurus (Gradien garis) dapat dilakukan dengan membagi perpindahan jarak  yang ditempuh secara vertikal (delta y) dengan perpindahan jarak yang ditempuh secara horisontal (delta x).

Misalkan mobil yang bergerak dari A0 menuju A1 berpindah sejauh 20 meter ke arah horisontal dan 30 meter ke arah vertikal, maka gradien garisnya adalah

Untuk membedakan jalan/garis menurun dengan garis yang naik/menanjak maka dibuat kesepakatan sebagai berikut:

1. Naik atau turun suatu garis ditentukan dengan bergerak dari kiri ke kanan. Jika dari kiri ke kanan ternyata garis menurun (posisi menjadi lebih rendah) maka gradien akan bertanda negatif. Sedangkan Jika dari kiri ke kanan ternyata garis naik (posisi menjadi lebih tinggi) maka gradien akan bertanda positif. 
2. Gradien disimbolkan dengan huruf m. Misalkan untuk kasus mobil hijau di atas, maka gradiennya adalah m = 3/2 (tanda positif karena jalan naik).

Gradien banyak digunakan pada geometri analitik terutama untuk menetukan persamaan garis pada bidang koordinat kartesius. Ada dua cara mencari gradien suatu garis pada koordinat kartesius yaitu:

1. Jika garis melalui titik origin O(0,0). Misalkan garis-garis berikut:

Pertama tentukan satu titik yang dilewati selain O(0,0) dan jelas ditentukan koordinatnya (pada gambar dibawah yaitu titik A(5,7) dan B(6,3)). Kemudian tentukan besar perpindahan pada arah horisontal (delta x) dan perpindaan pada arah vertikal (delta y) dengan acuan titik O sebagai awal dan A serta B sebagai akhir.

Secara Umum, Jika suatu garis lurus melalui titik O(0,0) dan suatu titik (a,b) maka gradiennya adalah:

     2.  Jika garis tidak melalui titik origin O(0,0). Misalkan garis berikut:

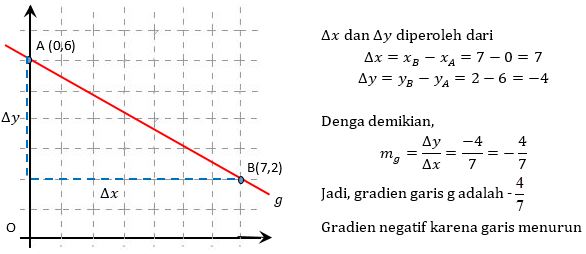
Untuk mencari gradiennya maka, pertama tentukan dua titik yang dilewati oleh garis misalkan titik A(0,6) dan B(7,2) (koordinat titik harus jelas jangan kira-kira). Titik tersebut menjadi acuan sebagai titik awal dan akhir sehingga kita bisa mencari delta x dan delta y nya.

Beberapa garis memiliki gradien yang spesial atau khusus. Garis tersebut adalah garis yang sejajar sumbu x dan garis yang sejajar sumbu Y. Gradien garis yang sejajar sumbu X adalah 0 sedangkan gradien garis yang sejajar dengan sumbu y adalah tak hingga (infinity).

Pada materi matematika SMA kelas X, gradien garis dapat pula dicari menggunakan fungsi trigonometri. Hal ini dikarenakan gradien garis pada bidang koordinate kartesius bergantung pada sudut yang dibentuk antara garis tersebut dan sumbu x. Bagaimana mencarinya?

Jadi gradien suatu garis lurus adalah sama dengan hasil tangen sudut anatara garis tersebut dengan sumbu x.

Contohnya:

Garis g, l memotong sumbu x dan membentuk sudut-sudut berikut:

 

Jika ada pertanyaan, kritik, atau saran silahkan tuliskan pada kolom komentar.

Demikianlah Artikel Gradien Garis Lurus: Derajat Kemiringan Garis

Itulah contoh soal ataupun materi pelajaran Gradien Garis Lurus: Derajat Kemiringan Garis, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sekian postingan pelajaran kali ini.

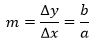
Anda sedang membaca artikel Gradien Garis Lurus: Derajat Kemiringan Garis dan artikel ini url permalinknya adalah https://rumuskelilinglingkaran.blogspot.com/2015/09/gradien-garis-lurus-derajat-kemiringan.html Semoga artikel ini bisa bermanfaat.

Tweet