Materi : Barisan Geometri Soal dan Pembahasan
Judul materi : Barisan Geometri Soal dan Pembahasan
Barisan Geometri Soal dan Pembahasan
Barisan Geometri Soal dan Pembahasan - Setelah pada kesempatan yang lalu kita telah membahas barisan dan deret aritmatika, saatnya kita ke materi selanjutnya yaitu geometri. Langsung saja sobat, mari kita langsung ke materi saja.Barisan Geometri
Barisan geometri merupakan barisan yang suku-sukunya diperoleh dengan mengalikan satu bilangan tetap ke suku sebelumnya. Bilangan tetap itu sering disebut sebagai pembanding atau rasio yang dilambangkan dengan r.
Barisan U1, U2 , U3 , U4 , ….. , Un disebut sebagai barisan geometri jika memenuhi

Contoh barisan geometri : 7, 21, 63, 189, ....
Rumus Suku ke-n
Jika suku pertama ( U1 ) dari suatu barisan geometri disimbolkan dengan a , maka rumus suku ke-n barisan geometri dapat ditentukan sebagai berikut:
Dari pernyataan diatas, dapat ditarik kesimpulan bahwa rumus suku ke-n dari suatu barisan geometri adalah
Dimana r adalah rasio atau pembanding yang dapat dicari dengan cara berikut:
Contoh Soal :
- Tentukan suku ke tujuh dari barisan geometri 3, 6, 12, .....!
- Tentukan Rumus Suku ke-n dari barisan 48 , 24 , 12 , ……!
- Dari barisan geometri diketahui bahwa U3 = 4 dan U9 = 256, maka tentukan U12!
- Tiga buah bilangan membentuk barisan geometri. Jumlah ketiga bilangan tersebut sama dengan 35, sedangkan hasil kali ketiga bilangan itu sama dengan 1.000. Maka tentukan barisan geometri tersebut!
Jawab :
1. Dari Barisan 3, 6, 12, ... didapat a = 3 dan r = 6/3 = 2 sehingga,
Un = a.rn-1
U7 = 3.27-1
U7 = 3.26
U7 = 3.64
U7 = 192
2. Dari barisan 48, 24, 12, .... didapat a = 48 dan r = 24/48 = 1/2 sehingga,Un = a.rn-1
Un = 48.(1/2)n-1
Un = 48.((2-1)n-1
Un = 3.16.21-n
U7 = 3.24.21-n
U7 = 3.25-n
3. Pertama, kita jabarkan terlebih dahulu U3 dan U9 kemudian kita cari nilai rasionyaU3 = 4 → a.r2 = 4
U9 = 256 → a.r8 = 256
Kemudian substitusikan untuk mencari U1 atau a!
→ a.r2 = 4
→ a.22 = 4
→ a = 1
Next, cari nilai U12 dengan menggunakan rumus umum barisan geometri!U12 = a.rn-1
U12 = 1.211
U12 = 1.2048
U12 = 2048Mungkin itu saja sobat informasi yang bisa saya berikan tentang Barisan Geometri Matematika semoga bermanfaat.
Demikianlah Artikel Barisan Geometri Soal dan Pembahasan
Itulah contoh soal ataupun materi pelajaran Barisan Geometri Soal dan Pembahasan, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sekian postingan pelajaran kali ini.



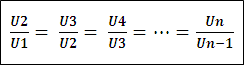

0 Response to "Barisan Geometri Soal dan Pembahasan"
Posting Komentar