Materi : Rumus Perbandingan Vektor
Judul materi : Rumus Perbandingan Vektor
Rumus Perbandingan Vektor
Baiklah, kali ini bertemu lagi dengan saya di Pelajaran Matematika, jadi akhirnya saya menemukan sesuatu yang sangat saya sukai, yaitu memposting tentang matematika. Meski sebenarnya dulunya saya memilih niche tekno, tetapi saya akhirnya lebih suka posting soal matematika dibanding lain nya karena memang matematika sangat dibutuhkan mulai dari anak SD hingga kuliah.
Saya sendiri sekarang kuliah di jurusan Sistem Informasi di Universitas Kanjuruhan Malang, dan ternyata di jurusan saya juga butuh matematika. Saya sering cari referensi dari Google, tetapi akhirnya saya memilih untuk membuat blog sendiri karena saya juga sambil belajar sambil main blog. Baiklah kali ini kita bertemu dengan rumus perbandingan vektor.
Rumus Perbandingan Vektor
 |
| Rumus Perbandingan Vektor |
Nobita pergi ke sekolah dengan berjalan kaki, ia melintasi sebuah jalan yang lurus. Jika saat ini Nobita telah meninggalkan rumah sejauh m meter dan Nobita harus menempuh jarak n meter lagi untuk tiba di sekolah, maka perbandingan jarak yang telah ditempuh Nobita dengan jarak yang belum ditempuhn Nobita adalah m : n.
Misalkan :
Posisi rumah Nobita adalah P
Posisi sekolah Nobita adalah Q
Posisi Nobita saat ini adalah N
Maka dapat dituliskan PN : NQ = m : n.
Dari perbandingan tersebut, teman-teman dapat menyatakan titik N sebagai vektor posisi n dalam vektor posisi titik P dan Q. Dengan cara sebagai berikut :
n = r + PN
n = r + (m/(m + n))PQ
n = r + (m/(m + n))(s - r)
n = (mr + nr + ms - mr)/(m + n)
n = (ms + nr)/(m + n)Maka n = (ms + nr)/(m + n)
n = r + (m/(m + n))PQ
n = r + (m/(m + n))(s - r)
n = (mr + nr + ms - mr)/(m + n)
n = (ms + nr)/(m + n)Maka n = (ms + nr)/(m + n)
- Jika P(x1, y1) dan Q(x2, y2) di R2, maka n = (m(x2, y2) + n(x1, y1))/(m + n).
Koordinat titik N adalah N((mx2 + nx1)/(m + n), (my2 + ny1)/(m + n)). - Jika P(x1, y1, z1) dan Q(x2, y2, z2) di R3, maka n = (m(x2, y2, z2)+ n(x1, y1, z1))/(m + n).
Koordinat titik N adalah N((mx2 + nx1)/(m + n), (my2 + ny1)/(m + n), (mz2 + nz1)/(m + n)).
1. Titik N membag PQ di dalam,
PN : NQ = m : n2. Titik N membagi PQ di luar.
PN : NQ = m : (-n) |
| Rumus Perbandingan Vektor |
Itulah rumus perbandingan vektor yang bisa kamu pelajari untuk hari ini, dan jangan lupa untuk cek postingan lain nya juga ya karena kami selalu mengupdate artikel setiap hari. Jadi budayakan tiada hari tanpa matematika agar kamu bisa mengerti matematika secara lengkap. Terima kasih sudah berkunjung di Rumus Keliling Lingkaran.
Demikianlah Artikel Rumus Perbandingan Vektor
Itulah contoh soal ataupun materi pelajaran Rumus Perbandingan Vektor, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sekian postingan pelajaran kali ini.


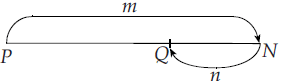
0 Response to "Rumus Perbandingan Vektor"
Posting Komentar